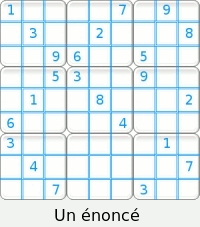
| Suite à la réglementation européenne sur la protéction de données (RGPD), nous vous informons que nous utilisons des cookies pour vous garantir la meilleure expérience sur ce site Web, pour personnaliser les publicités (qui permettent la gratuité de ce site) et pour analyser le trafic du site. Si ce message apparait sans arrêt à toutes ouvertures de pages cliquez sur "En savoir plus". En continuant à naviguer sur notre site, vous acceptez l'utilisation de ces cookies qui permettent de compiler des statistiques de visites et personnaliser les inserts publicitaires. Fermer En savoir plus Aide et technique de résolution Définitions des termes. Une grille sudoku complète est un tableau de 9 cases sur 9, subdivisé en 9 carrés de 3 cases de côté. Chaque case contient un seul chiffre allant de 1 à 9. Chaque ligne, colonne, et carré de 3 X 3 incluent obligatoirement ces 9 chiffres. Par conséquent, pris isolément, une ligne, une colonne ou un carré de 3 sur 3 ne peuvent contenir plusieurs fois une même valeur.
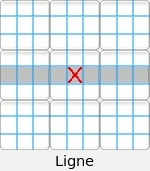
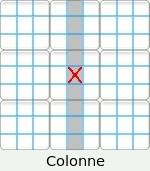
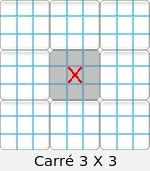
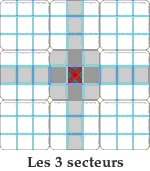
Nous appellerons « secteur d'une case » la ligne, la colonne ou la région carrée de 3 X 3 dans lesquels une case est incluse. Par exemple la case centrale appartient aux trois secteurs suivants :
Attention : Le terme « région » définit un carré de 3 X 3. Le terme « secteur » indique indifféremment la ligne, la colonne ou la région carrée afférente à une case. Méthodes de résolution. Nous ne développerons uniquement ci-dessous que les procédures utilisées par le résolveur du site. Nous rajouterons ultérieurement d'autres méthodes au fur et à mesure des améliorations du logiciel. Il y deux types principaux de méthode.• Celles solubles directement par un schéma visuel ou par la lecture des candidats. • Celles solubles exclusivement par la lecture des candidats. On appelle candidats d'une case les chiffres possibles que cette case peut admettre. L'ensemble des candidats d'un énoncé sudoku sont toutes les possibilités de toutes les cellules de la grille. Le site vous permet de les afficher à tout moment. Il est conseillé, pour faciliter la tâche, de commencer à résoudre visuellement le maximum de cases pour terminer avec le minimum de candidats à écrire. Les quatre méthodes de base : • Conduite par inclusion. Deux méthodes indirectes : Une pseudo méthode : • Conduite par choix multiple. La capacité des méthodes : |