| Suite à la réglementation européenne sur la protéction de données (RGPD), nous vous informons que nous utilisons des cookies pour vous garantir la meilleure expérience sur ce site Web, pour personnaliser les publicités (qui permettent la gratuité de ce site) et pour analyser le trafic du site. Si ce message apparait sans arrêt à toutes ouvertures de pages cliquez sur "En savoir plus". En continuant à naviguer sur notre site, vous acceptez l'utilisation de ces cookies qui permettent de compiler des statistiques de visites et personnaliser les inserts publicitaires. 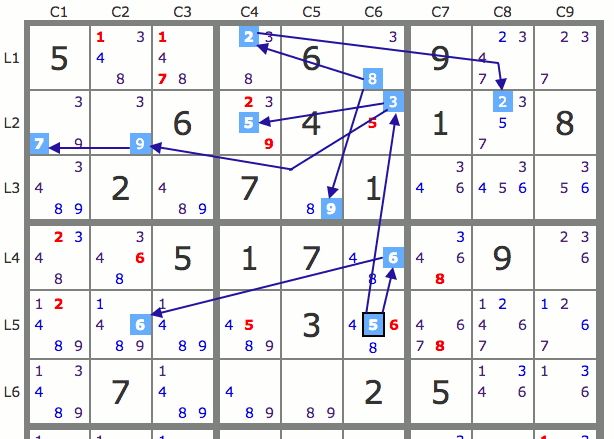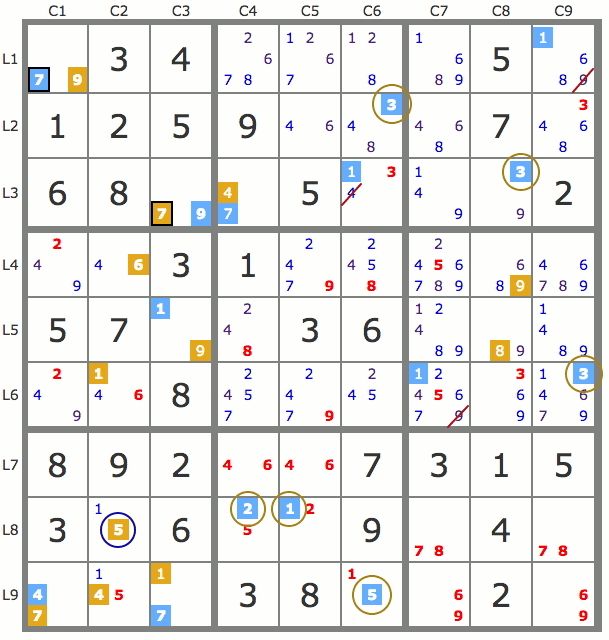Fermer En savoir plus Techniques des pistes Introduction La technique des pistes élaborée par Robert Mauriès s'applique aux grilles d'un niveau supérieur à 7 pour lesquelles les techniques de base (conduites par inclusion, exclusion et n-exclusives) deviennent insuffisantes. Son principe repose sur la construction de deux pistes, qui sont des suites de candidats, afin d'exploiter les propriétés d'interaction de ces deux pistes pour résoudre la grille. Définition d'une piste issue d'un candidat Une piste P issue d'un candidat A est l'ensemble des candidats qui seraient solutions de la grille "SI" le candidat A était solution de la grille. Par exemple, sur la grille de la figure 1, le candidat de départ de la piste à construire étant le 5L5C6, la piste est composée de tous les candidats coloriés en bleu.
En effet, si le 5L5C6 était solution, le 6L4C6 qui serait seul dans B5 serait solution, alors le 6L5C2 serait solution aussi, tandisque le 3 étant seul dans L2C6 serait aussi solution, donc le 8L1C6 aussi, etc... Marquage d’une piste Avec les logiciels, ou les applications internet ( http://www.assistant-sudoku.com), disposant d’un marquage des candidats par couleur, le marquage des candidats d’une piste est fait comme sur la figure 1 par un carré d’une même couleur (les flèches ne servant ici qu’à expliquer le cheminement suivi). Paire de candidats Dans les grilles de sudoku, même les plus difficiles, un certain nombre de candidats forment des paires (ou couples) au sens général suivant : Une paire (ou couple) est un couple de deux candidats qui, sont seuls à occuper une case, ou bien, ont la même valeur et sont les seuls de cette valeur dans une zone sudoku (bloc, ligne ou colonne).
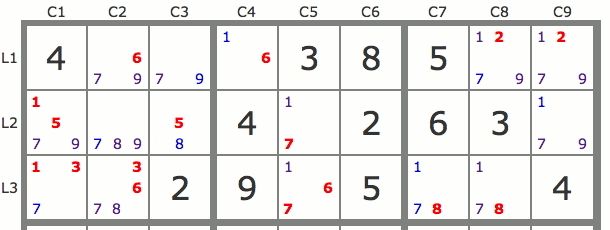
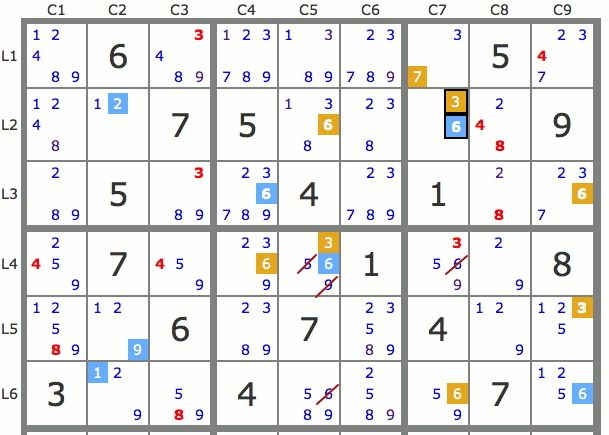
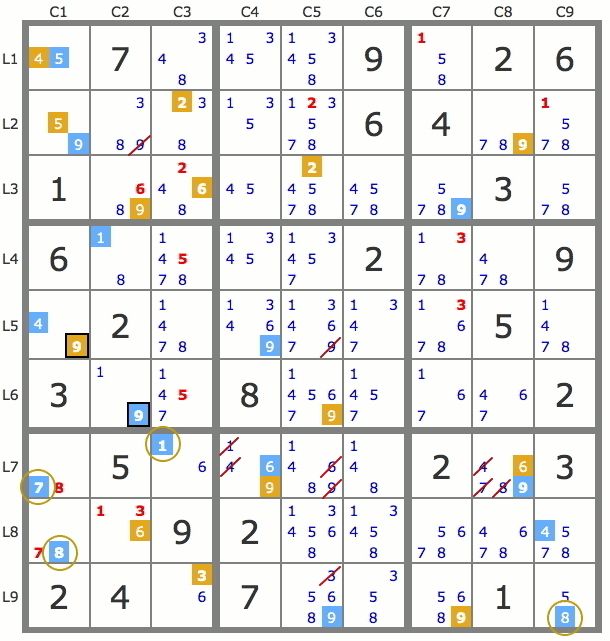
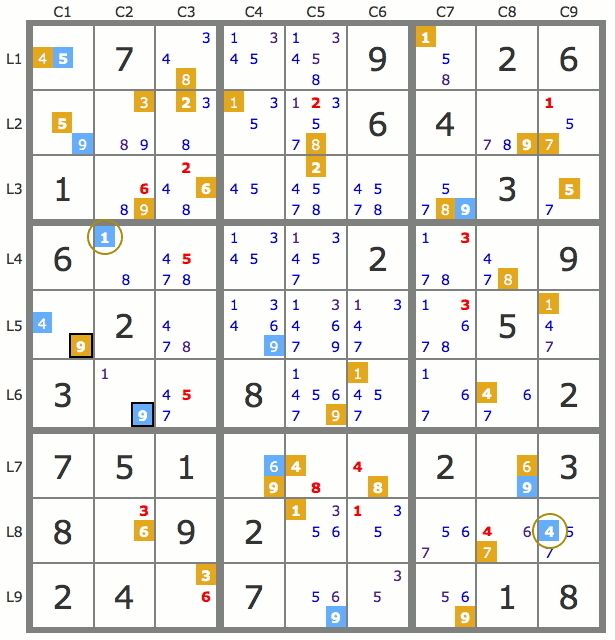
Sur la grille de la figure 2, les paires de candidats de même valeur sont portées en rouge, mais on voit aussi d’autres paires comme celles des couples 1/6 de L1C4, 7/9 de L1C3, 1/7 de L2C5 ou 5/8 de L2C3. Jeu de pistes issues d’une paire En traçant deux pistes issues respectivement de chacun des candidats d’une paire on peut résoudre partiellement ou totalement une grille, cela en raison des propriétés d’interaction suivantes : Propriété 1 : P1 et P2 étant respectivement les pistes issues des deux candidats d’une paire, tout candidat qui “voit” à la fois un candidat de P1 et un candidat de P2 peut être éliminé de la grille. Précisons un point de terminologie de cette propriété : On dit qu’un candidat “voit” un autre candidat lorsque, soit les deux candidats sont dans la même case, soit les deux candidats ont la même valeur et sont dans une même zone. Sur la grille de la figure 3 où l’on a tracé, au départ de la paire 36L2C7, une piste bleue issue du 6L2C7 et une piste jaune issue du 3L2C7, tous les candidats barrés en rouge peuvent être éliminés car ils voient des candidats des deux pistes.
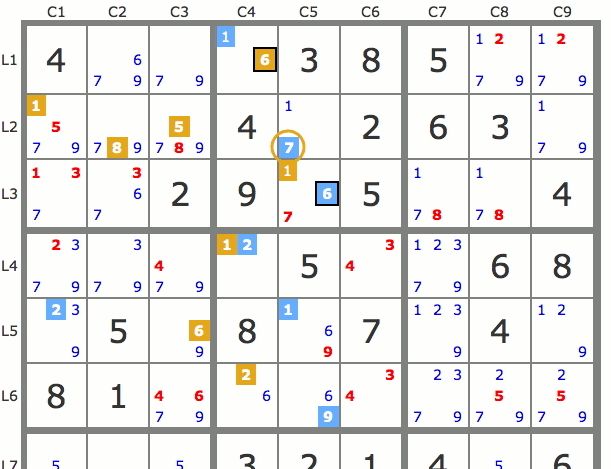
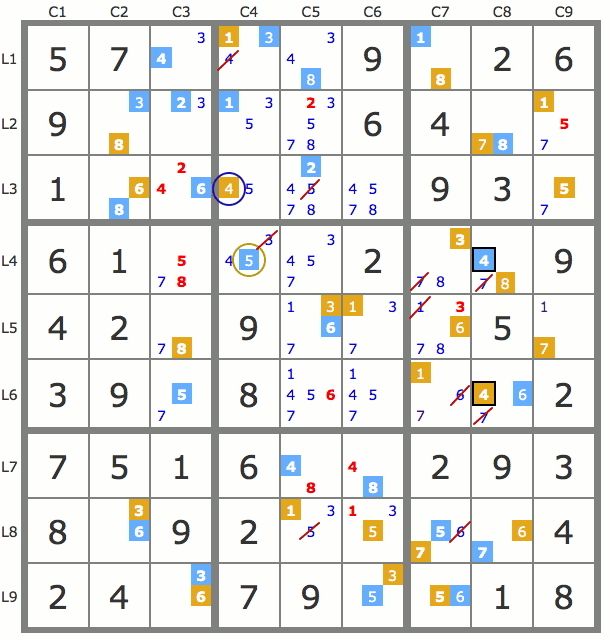
La propriété suivante est une conséquence de la précédente. Propriété 2 : P1 et P2 étant respectivement les pistes issues des deux candidats d’une paire, si les deux pistes ont en commun un même candidat dans une case, ce candidat est solution de la case. On dit que les deux pistes se croisent sur ce candidat. Par exemple sur la grille de la figure 4, les deux pistes issues des 6 de la paire de 6 du bloc 2 ont en commun le 7 de L2C5. Le 7 de L2C5 est donc solution de la grille.
Exemple de résolution d’une grille Voici un exemple de résolution d’une grille faisant appel aux propriétés énoncées dans le paragraphe précédent. Le choix de ces candidats a été fait parce que les deux pistes se développent plutôt bien, ce qui laisse penser que des interactions entre-elles simplifieront la grille.
Jeux de pistes successifs Si les interactions des deux pistes d’un premier jeu de pistes ne solutionne la grille que partiellement, on efface les deux pistes et on utilise un nouveau jeu de pistes au départ d’une autre paire de candidats, et ainsi de suite. Par exemple, la grille suivante de niveau 10/12 peut se résoudre avec deux jeux de pistes successifs.
On poursuit le développement de la piste jaune (figure 7) pour aboutir à deux autres placements par croisement des deux pistes (candidats entourés d’un rond), ce qui permet plusieurs placements par les technique de base.
Sur la grille largement simplifiée, on efface le premier jeu de pistes pour tracer un second jeu de pistes issues de la paire de 4 du bloc 6 (figure 8).
Pour en savoir plus La technique des pistes ne se résume pas à l’utilisation d’un ou plusieurs jeux de pistes issues d’une paire. D’autres notions et propriétés permettent de traiter les grilles les plus difficiles : invalidité d’une piste, pistes conjuguées, pistes opposées, bifurcations, etc... Le livre de Robert Mauriès “Technique des pistes en sudoku” expose tous les aspects de cette technique avec de nombreux exemples d’application.
|
